1.
问题情境:
定义:如果两个等腰三角形的顶角互补,顶角的顶点又是同一个点,而且这两个等腰三角形的腰也分别相等,则称这两个三角形互为“顶补等腰三角形”.
(1)
特例证明:
(2)
拓展运用:
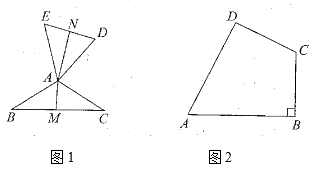
如图1,若与
互为“顶补等腰三角形”.
,
于
,
于
, 求证:
;
如图2,在四边形中,
,
,
,
, 在四边形
的内部是否存在点
, 使得
与
互为“顶补等腰三角形”?若存在,请给予证明;若不存在,请说明理由.
【考点】
等腰三角形的性质;
三角形全等的判定-SSS;
三角形全等的判定-AAS;
能力提升





