1.
阅读下列材料并解答问题:
在一个三角形中,如果一个内角的度数是另一个内角度数的3倍,那么这样的三角形我们称为“3倍角三角形”. 例如:一个三角形三个内角的度数分别是 , 这个三角形就是一个“3倍角三角形”. 反之,若一个三角形是“3倍角三角形”,那么这个三角形的三个内角中一定有一个内角的度数是另一个内角度数的3倍.

(1)
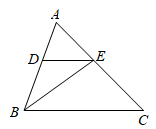
如图①,已知 , 在射线
, 在射线 上取一点
上取一点 , 过点
, 过点 作
作 交
交 于点
于点 , 判断
, 判断 是不是“3倍角三角形”,为什么?
(2)
在(1)的条件下,以
是不是“3倍角三角形”,为什么?
(2)
在(1)的条件下,以 为端点画射线
为端点画射线 , 交线段
, 交线段 于点
于点 (点
(点 不与点
不与点 、点
、点 重合),若
重合),若 是“3倍角三角形”,求
是“3倍角三角形”,求 的度数;
(3)
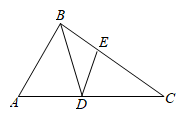
如图②,点
的度数;
(3)
如图②,点 在
在 的边上,连接
的边上,连接 , 作
, 作 的平分线交
的平分线交 于点
于点 , 在
, 在 上取一点
上取一点 , 使得
, 使得 , 若
, 若 是“3倍角三角形”,求
是“3倍角三角形”,求 的度数.
的度数.
【考点】
三角形内角和定理;
角平分线的概念;
能力提升
真题演练