已知∠MPN的两边分别与⊙O相切于点A，B，⊙O的半径为r．

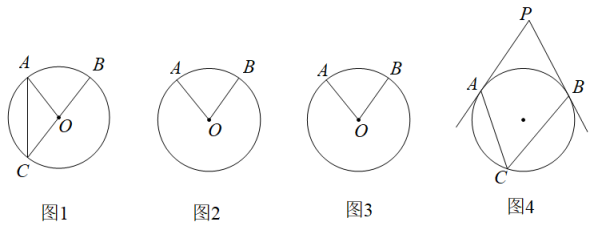
1. 已知∠MPN的两边分别与⊙O相切于点A，B，⊙O的半径为r．

(1) 如图1，点C在点A，B之间的优弧上，∠MPN=80°，求∠ACB的度数：

(2) 如图2，点C在圆上运动，当PC最大时，要使四边形APBC为菱形，∠APB的度数应为多少？请说明理由；

(3) 若PC交⊙O于点D，求第（2）问中对应的阴影部分的周长（用含r的式子表示），

【考点】

切线的性质; 圆的综合题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图1， $\text{[math]}$ 为 $\text{[math]}$ 的直径， $\text{[math]}$ 为弦，过圆心O作 $\text{[math]}$ 于D，点E为 $\text{[math]}$ 延长线上一点， $\text{[math]}$ 是 $\text{[math]}$ 的切线．

(1) 求证： $\text{[math]}$ ；

(2) 如图2，取弧 $\text{[math]}$ 的中点P，连接 $\text{[math]}$ ，若 $\text{[math]}$ ， $\text{[math]}$ ，求弦 $\text{[math]}$ 的长．

综合题普通

2. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的半径， $\text{[math]}$ 与 $\text{[math]}$ 相切于点A ，点C在 $\text{[math]}$ 上且 $\text{[math]}$ 为 $\text{[math]}$ 的中点，连接 $\text{[math]}$ ，连接 $\text{[math]}$ 交 $\text{[math]}$ 于点E ，交 $\text{[math]}$ 于点F ．

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的长．

综合题普通

3. 如图，AB是⊙O的直径，点P是弦AC上一动点（不与A，C重合），过点P作PE⊥AB，垂足为E，射线EP交 $\text{[math]}$ 于点F，交过点C的切线于点D．

(1) 求证：DC=DP；

(2) 若∠CAB=30°，当F是 $\text{[math]}$ 的中点时，判断以A，O，C，F为顶点的四边形是什么特殊四边形？说明理由．

综合题困难