0 返回首页
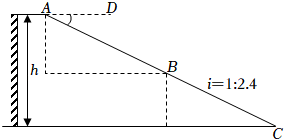
1. 2022年北京冬奥会的成功举办激发了人们对冰雪运动的热情．如图是某滑雪场的横截面示意图，雪道分为AB，BC两部分，小明同学在C点测得雪道BC的坡度i=1：2.4，在A点测得B点的俯角∠DAB=30°．若雪道AB长为270m，雪道BC长为260m．

(1) 求该滑雪场的高度h；
(2) 据了解，该滑雪场要用两种不同的造雪设备来满足对于雪量和雪质的不同要求，其中甲设备每小时造雪量比乙设备少35m3 ， 且甲设备造雪150m3所用的时间与乙设备造雪500m3所用的时间相等．求甲、乙两种设备每小时的造雪量．
【考点】
解直角三角形的实际应用﹣仰角俯角问题;
【答案】

您现在未登录，无法查看试题答案与解析。 登录
综合题 普通
能力提升
真题演练
换一批
1. 为庆祝改革开放40周年，深圳举办了灯光秀，某数学兴趣小组为测量“平安金融中心”AB的高度，他们在地面C处测得另一幢大厦DE的顶部E处的仰角∠ECD=32°.登上大厦DE的顶部E处后，测得“平安中心”AB的顶部A处的仰角为60°，（如图）.已知C、D、B三点在同一水平直线上，且CD=400米，DB=200米.

（参考数据：sin32°≈0.53，cos32°≈0.85，tan32°≈0.62， ≈1.41， ≈1.73）

(1) 求大厦DE的高度；
(2) 求平安金融中心AB的高度.
综合题 普通
2. 为了监控大桥下坡路段车辆行驶速度，通常会在下引桥处设置电子眼进行区间测速，如图，电子眼位于点P处，离地面的铅锤高度PQ为9米，区间测速的起点为下引桥坡面点A处，此时电子眼的俯角为30°；区间测速的中点为下引桥坡脚点B处，此时电子眼的俯角为60°（A、B、P、Q四点在同一平面）．

(1) 求路段BQ的长（结果保留根号）；
(2) 当下引桥坡度 时，求电子眼区间测速路段AB的长（结果保留根号）．
综合题 普通
3. 如图，线段AB、CD分别表示甲乙两建筑物的高，BA⊥AD，CD⊥DA，垂足分别为A、D．从D点测到B点的仰角α为60°，从C点测得B点的仰角β为30°，甲建筑物的高AB=30米

(1) 求甲、乙两建筑物之间的距离AD．
(2) 求乙建筑物的高CD．
综合题 普通