1.
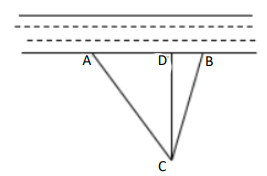
在一条东西走向河的一侧有一村庄  ,河边原有两个取水点
,河边原有两个取水点  ,其中
,其中  ,由于某种原因,由
,由于某种原因,由  到
到  的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点
的路现在已经不通,该村为方便村民取水决定在河边新建一个取水点  在同一条直线上),并新修一条路
在同一条直线上),并新修一条路  ,测得
,测得  千米,
千米,  千米,
千米,  千米.
千米.
(1)
问  是否为从村庄
是否为从村庄  到河边最近的路?请通过计算加以说明:
(2)
求原来的路线
到河边最近的路?请通过计算加以说明:
(2)
求原来的路线  的长.
的长.
【考点】
轴对称的应用-最短距离问题;