1.
在平面直角坐标系中,已知抛物线  与
与  轴交于
轴交于  ,
,  两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
两点(点A在点B的左侧),与y轴交于点C,顶点为点D.
(1)
当  时,直接写出点A,B,C,D的坐标:
(2)
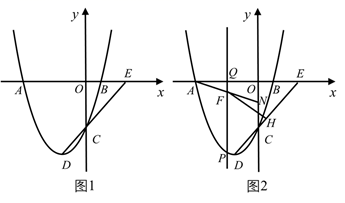
如图1,直线
时,直接写出点A,B,C,D的坐标:
(2)
如图1,直线  交x轴于点E,若
交x轴于点E,若  ,求a的值和
,求a的值和  的长;
(3)
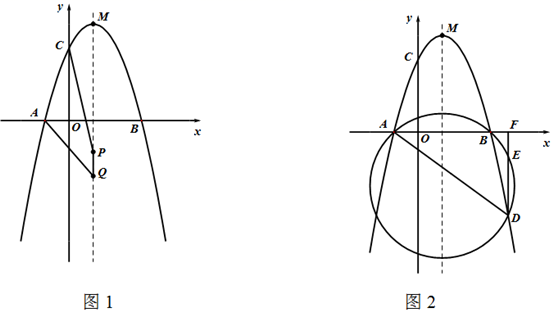
如图2,在(2)的条件下,若点N为
的长;
(3)
如图2,在(2)的条件下,若点N为  的中点,动点P在第三象限的抛物线上,过点P作x轴的垂线,垂足为Q,交
的中点,动点P在第三象限的抛物线上,过点P作x轴的垂线,垂足为Q,交  于点F;过点F作
于点F;过点F作  ,垂足为H.设点P的横坐标为t,记
,垂足为H.设点P的横坐标为t,记  .
.
,
,
,
;
①用含t的代数式表示f;
②设 ,求f的最大值.
【考点】
二次函数-动态几何问题;
能力提升
真题演练