1.
如图,已知AB∥DC,ED∥BC,AE∥BD,那么图中与三角形ABD面积相等的三角形共有个.
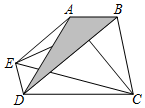
【考点】
平行线之间的距离;
三角形的面积;
基础巩固
能力提升
变式训练
拓展培优
真题演练