1.
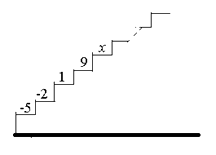
如图,阶梯图的每个台阶上都标着一个数,从下到上的第1个至第4个台阶上依次标着-5,-2,1,9,且任意相邻四个台阶上数的和都相等.
(1)
求前4个台阶上数的和是多少?
(2)
求第5个台阶上的数  是多少?
(3)
应用 求从下到上前31个台阶上数的和.
是多少?
(3)
应用 求从下到上前31个台阶上数的和.
发现 试用含k(k为正整数)的式子表示出数“1”所在的台阶数.
【考点】
用字母表示数;
探索数与式的规律;
探索图形规律;
能力提升






