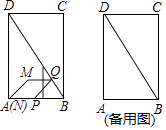
如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2 cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm2）

1. 如图，在矩形ABCD中，AB=2cm，∠ADB=30°．P，Q两点分别从A，B同时出发，点P沿折线AB﹣BC运动，在AB上的速度是2cm/s，在BC上的速度是2 $\text{[math]}$ cm/s；点Q在BD上以2cm/s的速度向终点D运动，过点P作PN⊥AD，垂足为点N．连接PQ，以PQ，PN为邻边作▱PQMN．设运动的时间为x（s），▱PQMN与矩形ABCD重叠部分的图形面积为y（cm²）

(1) 当PQ⊥AB时，x=；

(2) 求y关于x的函数解析式，并写出x的取值范围；

(3) 直线AM将矩形ABCD的面积分成1：3两部分时，直接写出x的值．

【考点】

平行四边形的性质; 相似三角形的判定与性质; 锐角三角函数的定义; 同角三角函数的关系; 四边形-动点问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，在锐角三角形ABC中，点D，E分别在边AC，AB上，AG⊥BC于点G，AF⊥DE于点F，∠EAF=∠GAC．

(1) 求证：△ADE∽△ABC；

(2) 若AD=3，AB=5，求 $\text{[math]}$ 的值．

综合题普通

2. 如图，点 $\text{[math]}$ 为 $\text{[math]}$ 的边 $\text{[math]}$ 延长线上一点， $\text{[math]}$ 与 $\text{[math]}$ 交于点 $\text{[math]}$ ，与 $\text{[math]}$ 交于点 $\text{[math]}$ .

(1) 求证： $\text{[math]}$ ；

(2) 若 $\text{[math]}$ ，求 $\text{[math]}$ 的长度.

综合题普通

3. 如图所示，延长平行四边形ABCD一边BC至点F，连结AF交CD于点E，若 $\text{[math]}$ ．

(1) 若BC＝3，求线段CF的长；

(2) 若△ADE的面积为1，求平行四边形ABCD的面积．

综合题普通