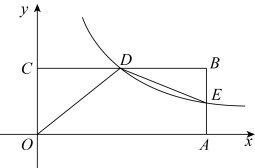
矩形AOBC中，OB=4，OA=3．分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系．F是BC边上一个动点（不与B，C重合），过点F的反比例函数y= （k＞0）的图象与边AC交于点E．

1. 矩形AOBC中，OB=4，OA=3．分别以OB，OA所在直线为x轴，y轴，建立如图1所示的平面直角坐标系．F是BC边上一个动点（不与B，C重合），过点F的反比例函数y= $\text{[math]}$ （k＞0）的图象与边AC交于点E．

(1) 当点F运动到边BC的中点时，求点E的坐标；

(2) 连接EF，求∠EFC的正切值；

(3) 如图2，将△CEF沿EF折叠，点C恰好落在边OB上的点G处，求此时反比例函数的解析式．

【考点】

待定系数法求反比例函数解析式; 矩形的性质; 翻折变换（折叠问题）; 相似三角形的判定与性质; 反比例函数图象上点的坐标特征;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 设函数 $\text{[math]}$ ，函数 $\text{[math]}$ （ $\text{[math]}$ ， $\text{[math]}$ ， b是常数， $\text{[math]}$ ， $\text{[math]}$ ）．若函数 $\text{[math]}$ 和函数 $\text{[math]}$ 的图象交于点 $\text{[math]}$ ，点 $\text{[math]}$ ．

(1) 求点 $\text{[math]}$ ， $\text{[math]}$ 的坐标．

(2) 求函数 $\text{[math]}$ ， $\text{[math]}$ 的表达式．

(3) 当 $\text{[math]}$ 时，直接写出 $\text{[math]}$ 的取值范围．

综合题普通

2. 如图，在平面直角坐标系 $\text{[math]}$ 中，矩形 $\text{[math]}$ 的顶点A，C分别在x轴，y轴上，D是BC的中点，过点D的反比例函数 $\text{[math]}$ 的图象交AB于点E，连接DE．若 $\text{[math]}$ ， $\text{[math]}$ ．

(1) 求反比例函数的解析式；

(2) 若点P在x轴上，且以P，A，E为顶点的三角形是等腰直角三角形，请直接写出P点坐标．

综合题普通

3. 如图，大、小两个正方形的中心均与平面直角坐标系的原点O重合，边分别与坐标轴平行，反比例函数 $\text{[math]}$ 的图象与大正方形的一边交于点A(1，2)，且经过小正方形的顶点B.

(1) 求反比例函数的解析式；

(2) 求图中阴影部分的面积.

综合题普通