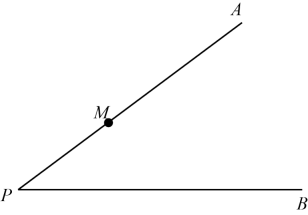
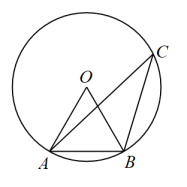
下面是“作一个角”的尺规作图过程.已知：平面内一点 .求作：，使得 .作法：如图，①作射线；②在射线上取一点，以为圆心，为半径作圆，与射线相交于点；③以为圆心，为半径作孤，与交于点，作射线 . 即为所求的角.请回答：该尺规作图的依据是．

1. 下面是“作一个 $\text{[math]}$ 角”的尺规作图过程.

已知：平面内一点 $\text{[math]}$ .

求作： $\text{[math]}$ ，使得 $\text{[math]}$ .

作法：如图，

①作射线 $\text{[math]}$ ；

②在射线 $\text{[math]}$ 上取一点 $\text{[math]}$ ，以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作圆，与射线 $\text{[math]}$ 相交于点 $\text{[math]}$ ；

③以 $\text{[math]}$ 为圆心， $\text{[math]}$ 为半径作孤，与 $\text{[math]}$ 交于点 $\text{[math]}$ ，作射线 $\text{[math]}$ . $\text{[math]}$ 即为所求的角.

请回答：该尺规作图的依据是．

【考点】

等边三角形的判定与性质; 圆周角定理; 尺规作图-作一个角等于已知角;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，已知 $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ ， $\text{[math]}$ 是 $\text{[math]}$ 上的点，且位于直径 $\text{[math]}$ 的两侧，连接 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ．若 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为．

填空题容易

2. 如图， $\text{[math]}$ 内接于 $\text{[math]}$ 是 $\text{[math]}$ 的直径，连接BD，AO．已知 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是.

填空题容易

3. 如图， $\text{[math]}$ 内接于 $\text{[math]}$ 是 $\text{[math]}$ 的直径，连接 $\text{[math]}$ ．已知 $\text{[math]}$ ，则 $\text{[math]}$ 的度数是．

填空题容易