1.
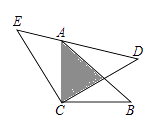
如图，△ACB和△ECD都是等腰直角三角形，CA=CB，CE=CD，△ACB的顶点A在△ECD的斜边DE上，若AE= 
，AD= 
，则两个三角形重叠部分的面积为（ ）
A.
B.
C.
D.
【考点】
三角形的面积;
全等三角形的判定与性质;
勾股定理;
相似三角形的判定与性质;
等腰直角三角形;
