1.
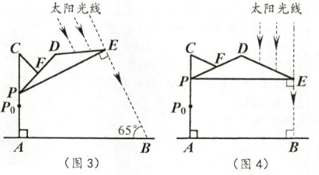
如图1,滑动调节式遮阳伞的立柱AC垂直于地面AB,P为立柱上的滑动调节点,伞体的截面示意图为△PDE,F为PD中点,AC=2.8m,PD=2m,CF=1m,∠DPE=20°。当点P位于初始位置P0时,点D与C重合(图2),根据生活经验,当太阳光线与PE垂直时,遮阳效果最佳。
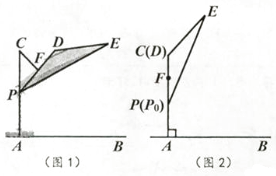
(1)
上午10:00时,太阳光线与地面的夹角为65°(图3),为使遮阳效果最佳,点P需从P0上调多少距离?(结果精确到0.1m)
(2)
中午12:00时,太阳光线与地面垂直(图4),为使遮阳效果最佳,点P在(1)的基础上还需上调多少距离?(结果精确到0.1m)
(参考数:sin70°≈0.94,cos70°≈0.34,tan70°≈2.75, ≈1.41,
≈1.73)
【考点】
等腰三角形的判定与性质;
解直角三角形;