1.
如图,在四棱锥P-ABCD中,底面ABCD为矩形,平面PAD⊥平面ABCD , PA⊥PD , PA=PD , E , F分别为AD , PB的中点.
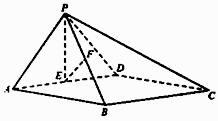
(Ⅰ)求证:PE⊥BC;
(Ⅱ)求证:平面PAB⊥平面PCD;
(Ⅲ)求证:EF∥平面PCD.
【考点】
空间中直线与直线之间的位置关系;
直线与平面平行的性质;
平面与平面垂直的判定;