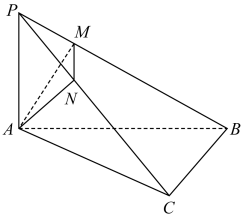
如图，在三菱柱ABC- 中，平面ABC。 D，E，F，G分别为，AC，，的中点，AB=BC= ，AC= =2。（Ⅰ）求证：AC⊥平面BEF：（Ⅱ）求二面角B-CD- 1的余弦值：（Ⅲ）证明：直线FG与平面BCD相交。

1. 如图，在三菱柱ABC- $\text{[math]}$ 中， $\text{[math]}$ 平面ABC。 D，E，F，G分别为 $\text{[math]}$ ，AC， $\text{[math]}$ ， $\text{[math]}$ 的中点，AB=BC= $\text{[math]}$ ，AC= $\text{[math]}$ =2。

（Ⅰ）求证：AC⊥平面BEF：

（Ⅱ）求二面角B-CD- $\text{[math]}$ ₁的余弦值：

（Ⅲ）证明：直线FG与平面BCD相交。

【考点】

反证法; 直线与平面垂直的判定; 与二面角有关的立体几何综合题; 二面角及二面角的平面角;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 已知 $\text{[math]}$ 的斜边为AB，过点A作PA⊥平面ABC，AM⊥PB于M，AN⊥PC于N.求证：

(1) BC⊥平面PAC；

(2) PB⊥平面AMN.

解答题普通

2. 设函数 $\text{[math]}$ 的最大值为M.

(2) 若正数a ， b满足 $\text{[math]}$ ，请问：是否存在正数a ， b ，使得 $\text{[math]}$ ，并说明理由.

解答题普通

3. 已知集合 $\text{[math]}$ ，且 $\text{[math]}$ 中的元素个数 $\text{[math]}$ 大于等于5.若集合 $\text{[math]}$ 中存在四个不同的元素 $\text{[math]}$ ，使得 $\text{[math]}$ ，则称集合 $\text{[math]}$ 是“关联的”，并称集合 $\text{[math]}$ 是集合 $\text{[math]}$ 的“关联子集”；若集合 $\text{[math]}$ 不存在“关联子集”，则称集合 $\text{[math]}$ 是“独立的”.

(1) 分别判断集合 $\text{[math]}$ 和集合 $\text{[math]}$ 是“关联的”还是“独立的”？若是“关联的”，写出其所有的关联子集；

(2) 已知集合 $\text{[math]}$ 是“关联的”，且任取集合 $\text{[math]}$ ，总存在 $\text{[math]}$ 的关联子集 $\text{[math]}$ ，使得 $\text{[math]}$ .若 $\text{[math]}$ ，求证： $\text{[math]}$ 是等差数列；

(3) 集合 $\text{[math]}$ 是“独立的”，求证：存在 $\text{[math]}$ ，使得 $\text{[math]}$ .

解答题普通