“像”的数学思考

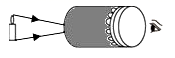
用如图1所示的自制简易针孔照相机的孔对准窗外的景物,在塑料薄膜上可看到一个倒立的像,小孔此现象就是小孔成像现象。关于小孔成像可构建如图2所示的理论模型:将光源看成许多点光源的集合体,每个点光源都会发出一条具有代表性的光线,在光屏上得到对应的像点。因此,光屏上呈现出由一个个像点组成的图样,即光源的倒立的“像”。由于此模型不考虑小孔的几何尺寸,将小孔视作理想的点,故称为小孔成像的理想化模型。
实际上,小孔必然存在一定的尺寸大小,所以物点会在光屏上形成光斑而不是光点。如图3所示,光斑的形状反映了小孔的形状,当孔径较大时,相邻光斑之间就会互相交叠,导致“像”的失真。在不同孔径、物距、像距下,“像”的形状可能与光源的形状相似,也可能与孔的形状相似。
选取光源在竖直方向上的线段进行研究,记线段长度为h,u、v分别表示物距和像距。图2是小孔成像的理想模型,不考虑小孔的尺寸,则所成“像”的形状应该与光源形状严格一致,“像”的大小仅仅取决于像距和物距的比值。可以将这一比值定义为像的理想缩放倍数
, 即
。图3中的小孔直径为d,则光源
在光屏上能照亮的全部范围是
。此时,像的实际缩放倍数为
, 即
。我们还可定义实际缩放倍数对理想缩放倍数的变化量与理想缩放倍数的比值为像对物体的形变率
, 可得出
的表达式为
, 可知
值取决于两个比例,即孔径与物径之比和物距和像距之比。
凸透镜成像也可以构建类似的模型,图4就是利用三条特殊光线构建的凸透镜成倒立缩小实像时的光学模型。凸透镜成像与小孔成像有很多相似之处,也有本质上的不同,例如,移走光屏,人眼只要在合适的位置是可以直接看到凸透镜所成的实像,但小孔成的像却不能。

信息快递: 从数学上来说,相似指两个图形的形状完全相同,其中一个图形能通过放大缩小的方式变成另一个。相似比是指两个相似图形的对应边的比值相等,其对应高的比也等于相似比。如图5,
|
 B.
B.
 C.
C.
 D.
D.












 小孔成像
小孔成像 阳光经物体表面到人眼
阳光经物体表面到人眼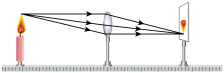 凸透镜成像
凸透镜成像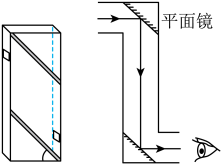 简易潜望镜
简易潜望镜