1.
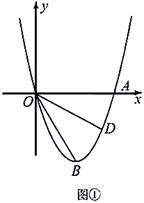
如图①,二次函数 的图象
的图象 与开口向下的二次函数图象
与开口向下的二次函数图象 均过点
均过点 ,
,  .
.

(1)
求图象 对应的函数表达式;
(2)
若图象
对应的函数表达式;
(2)
若图象 过点
过点 , 点P位于第一象限,且在图象
, 点P位于第一象限,且在图象 上,直线l过点P且与x轴平行,与图象
上,直线l过点P且与x轴平行,与图象 的另一个交点为Q(Q在P左侧),直线l与图象
的另一个交点为Q(Q在P左侧),直线l与图象 的交点为M,N(N在M左侧).当
的交点为M,N(N在M左侧).当 时,求点P的坐标;
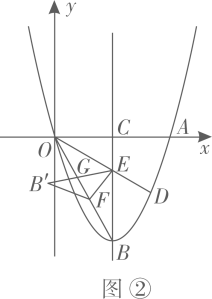
(3)
如图②,D,E分别为二次函数图象
时,求点P的坐标;
(3)
如图②,D,E分别为二次函数图象 ,
,  的顶点,连接
的顶点,连接 , 过点A作
, 过点A作 . 交图象
. 交图象 于点F,连接EF,当
于点F,连接EF,当 时,求图象
时,求图象 对应的函数表达式.
对应的函数表达式.
【考点】
待定系数法求二次函数解析式;
矩形的性质;
解直角三角形;