如图，在△ABC中，AB=AC，∠BAC=90°.D是直线AB上的一动点(不与点A，B重合)，BE⊥CD于点E，交直线AC于点F.

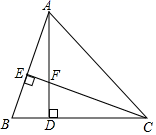
1. 如图，在△ABC中，AB=AC，∠BAC=90°.D是直线AB上的一动点(不与点A，B重合)，BE⊥CD于点E，交直线AC于点F.

(1) 当点D在边AB上时，试探究线段BD，AB和AF的数量关系，并证明你的结论.

(2) 若点D在AB的延长线或反向延长线上时，请你判断(1)中的结论是否仍成立.若成立，给出证明；若不成立，请画出图形并直接写出正确结论.

【考点】

三角形全等的判定-ASA; 线段的和、差、倍、分的简单计算;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 如图，阳阳为了测量楼高 $\text{[math]}$ ，在旗杆 $\text{[math]}$ 与楼之间选定一点 $\text{[math]}$ ，使 $\text{[math]}$ ，量得点 $\text{[math]}$ 到楼底距离 $\text{[math]}$ 与旗杆高度 $\text{[math]}$ 都为 $\text{[math]}$ ，旗杆与楼之间的距离 $\text{[math]}$ ，求楼高 $\text{[math]}$ ．

综合题普通

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边的中点，过点A作 $\text{[math]}$ 交 $\text{[math]}$ 的延长线于点 $\text{[math]}$ 平分 $\text{[math]}$ 交 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上一点，连接 $\text{[math]}$ ，且 $\text{[math]}$ ．求证：

(1) $\text{[math]}$ $\text{[math]}$ ；

(2) $\text{[math]}$ ．

综合题困难

3. 如图所示，在△ABC中，AD⊥BC于D，CE⊥AB于E，AD与CE交于点F，且AD＝CD.

(1) 求证：△ABD≌△CFD；

(2) 已知BC＝9，AD＝6，求AF的长.

综合题普通