1.
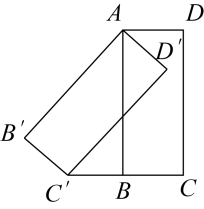
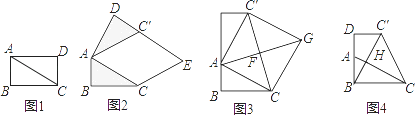
如图,已知 中,
中, , 先把
, 先把 绕点B顺时针旋转
绕点B顺时针旋转 至
至 后,再把
后,再把 沿射线平移至
沿射线平移至 相交于点H.
相交于点H.

(1)
判断线段 的位置关系,并说明理由;
(2)
连接
的位置关系,并说明理由;
(2)
连接 , 求证:四边形
, 求证:四边形 是正方形.
是正方形.
【考点】
正方形的判定;
平移的性质;
旋转的性质;