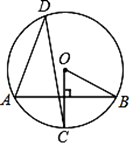
如图所示，点D是弦的中点，点C在上，经过圆心O，则下列结论中不一定正确的是（）

1. 如图所示，点D是弦 $\text{[math]}$ 的中点，点C在 $\text{[math]}$ 上， $\text{[math]}$ 经过圆心O，则下列结论中不一定正确的是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. 弧 $\text{[math]}$ 弧 $\text{[math]}$

【考点】

垂径定理的实际应用; 圆周角定理;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 如图，圆的两条弦AB，CD相交于点E，且 $\text{[math]}$ ，则 $\text{[math]}$ 的度数为（）

A. 50° B. 80° C. 70° D. 90°

单选题容易

2. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ ，则 $\text{[math]}$ （）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

3. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的内接三角形， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ ，则 $\text{[math]}$ （　　）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易