1.
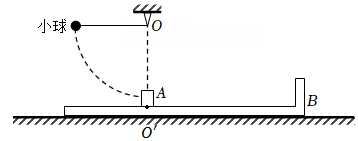
如图所示为一轨道模型图,由水平轨道AB、固定凹槽BGHC(GH足够长)、半圆轨道DE(D是最高点,E是最低点,C在D的正下方,且C和D间隙不计)组成,其中半圆轨道DE的半径R大小可调,所有轨道及凹槽均光滑。长度L=0.5m的水平传送带EF与DE平滑衔接。质量M=0.2kg的平板紧靠凹槽侧璧BG放置,平板上表面与ABC平面齐平。质量m=0.1kg的小滑块(可视为质点)被弹簧弹出后,滑上平板并带动平板一起运动,平板与侧璧CH相撞后将原速弹回。已知ABC平面与水平地面高度差h=1m,传送带顺时针传送速度v=1m/s,滑块与平板和传送带之间的动摩擦因数均为μ=0.4。

(1)
调节半圆轨道DE的半径为R=0.4m,被弹出的滑块恰好能滑过凹槽,且恰好不脱离圆轨道DE,求:
(2)
在保持问(1)中其他条件不变的情形下,仅改变R大小,滑块从F飞出落至地面,水平位移为x,求x的最大值。
①小滑块沿圆轨道滑过E点时受到的支持力FN;
②平板的长度及弹簧释放的弹性势能Ep。
【考点】
碰撞模型;
能力提升
真题演练