1.
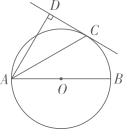
如图,地面上放着一个小凳子( 与地面平行),点A到墙面(墙面与地面垂直)的距离为
与地面平行),点A到墙面(墙面与地面垂直)的距离为 . 在图①中,一木杆的一端与墙角O重合,另一端靠在点A处,
. 在图①中,一木杆的一端与墙角O重合,另一端靠在点A处, .
.

(1)
求小凳子的高度;
(2)
在图②中另一木杆的一端与点B重合,另一端靠在墙上的点C处.若 , 木杆
, 木杆 比凳宽
比凳宽 长
长 , 求小凳子宽
, 求小凳子宽 和木杆
和木杆 的长度.
的长度.
【考点】
勾股定理;