1.
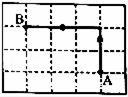
一个平面在空间中发生运动，可以形成立体图形。在生活中，我们经常见到类似的事情。例如：把铁锹看作近似的平面，将它垂直向下插入松软的沙土地，再沿水平方向推动铁锹，就会留下一个立体的坑。这样的现象在数学中叫作“面动成体”。要将如图中的平面运动起来，形成圆柱M的形状，下列做法错误的是（ ）
A.
将正方形绕直线l旋转180°。
B.
将长方形绕直线m旋转360°。
C.
将圆沿直线n向下平移2格。
D.
将三角形绕直线o旋转360°。
【考点】
将简单图形平移或旋转一定的度数;
基础巩固
能力提升
变式训练
拓展培优
真题演练
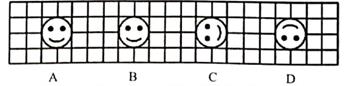
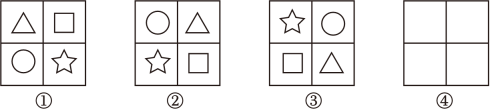
绕点O顺时针旋转90°后得到的图形是（ ）
