1.
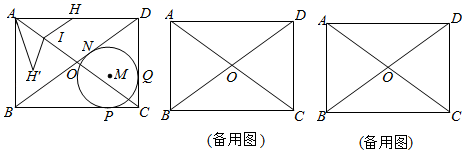
如图,已知A、B、C、D为矩形的四个顶点, ,
,  , 动点P、Q分别从点A、C同时出发,点P以
, 动点P、Q分别从点A、C同时出发,点P以 的速度向点B移动,一直到点B为止,点Q以
的速度向点B移动,一直到点B为止,点Q以 的速度向点D移动.问:
的速度向点D移动.问:

(1)
P、Q两点从出发开始几秒时,四边形 的面积为
的面积为 ?
(2)
几秒时点P点Q间的距离是10厘米?
(3)
P,Q两点间距离何时最小?
?
(2)
几秒时点P点Q间的距离是10厘米?
(3)
P,Q两点间距离何时最小?
【考点】
勾股定理;
四边形-动点问题;
能力提升
真题演练