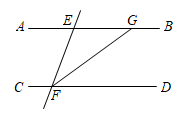
1.
将一副直角三角板如图摆放,即两个直角顶点重合,边 在三角板
在三角板 的“内部”,三角板
的“内部”,三角板 在直线
在直线 的上方.设
的上方.设 ,
,  ,
,  .
.

(1)
探究 与
与 的数量关系;
(2)
探究
的数量关系;
(2)
探究 与
与 的数量关系;
(3)
当这幅三角板出现两边平行时,求
的数量关系;
(3)
当这幅三角板出现两边平行时,求 的大小.
的大小.
【考点】
角的运算;
平行线的性质;
能力提升
真题演练