1.
综合与实践
某实践探究小组在放风筝时想测量风箏离地面的垂直高度,通过勘测,得到如下记录表:
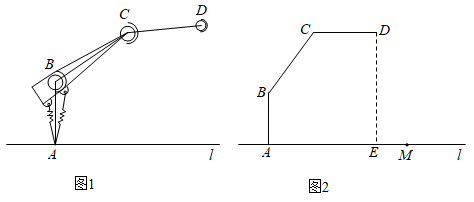
测量示意图 |
| |
测量数据 | 边的长度 | ①测得水平距离 |
②根据手中剩余线的长度计算出风筝线 | ||
③小明牵线放风筝的手到地面的距离为1.7米. | ||
数据处理组得到上面数据以后做了认真分析,他们发现根据勘测组的全部数据就可以计算出风筝离地面的垂直高度 . 请完成以下任务.
(1)
已知:如图,在 中,
中, ,
,  ,
,  . 求线段
. 求线段 的长.
(2)
如果小明想要风筝沿
的长.
(2)
如果小明想要风筝沿 方向再上升12米,
方向再上升12米, 长度不变,则他应该再放出多少米线?
长度不变,则他应该再放出多少米线?
【考点】
勾股定理的应用;
能力提升
真题演练