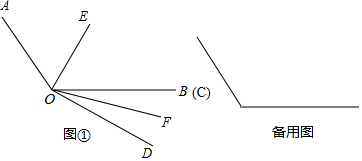
1.
如图1,一块三角板如图放置, , 直线
, 直线 分别交
分别交 于点
于点 ,
,  的角平分线
的角平分线 交
交 于点
于点 , 交
, 交 于点
于点 是线段
是线段 上的一点(不与
上的一点(不与 重合),连接
重合),连接 交
交 于点
于点 。
。

(1)
判断 之间的关系,并说明理由。
(2)
若
之间的关系,并说明理由。
(2)
若 , 用含
, 用含 的代数式表示
的代数式表示 的度数。
(3)
当
的度数。
(3)
当 时,将
时,将 绕着点
绕着点 以每秒
以每秒 的速度逆时针旋转,旋转时间为
的速度逆时针旋转,旋转时间为 , 当
, 当 边与射线
边与射线 重合时停止,则在旋转过程中,当
重合时停止,则在旋转过程中,当 的其中一边与
的其中一边与 的某一边平行时,求出此时
的某一边平行时,求出此时 的值。
的值。
【考点】
角平分线的概念;
内错角相等,两直线平行;
两直线平行,内错角相等;