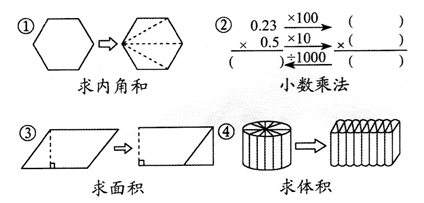
1.
在求“四边形的内角和”时,我们可以多角度去思考,用多种方法计算出四边形的内角和。

(1)
小明在研究六边形的内角和时,用了如图①的方法,请你按他的思路列式计算。
(2)
你还有和小明不一样的方法吗?在图②中画一画,并列式计算。

【考点】
多边形的内角和;