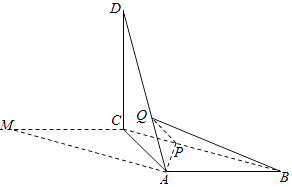
如图所示，长方形ABCD中，，，点M是边CD的中点，将沿AM翻折到，连接PB ， PC ，得到图的四棱锥．

1. 如图所示，长方形ABCD中， $\text{[math]}$ ， $\text{[math]}$ ，点M是边CD的中点，将 $\text{[math]}$ 沿AM翻折到 $\text{[math]}$ ，连接PB ， PC ，得到图的四棱锥 $\text{[math]}$ ．

(1) 求四棱锥 $\text{[math]}$ 的体积的最大值；

(2) 若棱PB的中点为N ，求CN的长；

【考点】

棱柱、棱锥、棱台的体积; 平面与平面垂直的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图，已知在正四棱锥 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ．

求四棱锥 $\text{[math]}$ 的表面积；

(1) 求四棱锥 $\text{[math]}$ 的体积．

解答题普通

(1) 已知正四棱锥的底面边长是 $\text{[math]}$ ，侧棱长为 $\text{[math]}$ ，求该正四棱锥的体积；

(2) 如图 $\text{[math]}$ 单位： $\text{[math]}$ ，求图中阴影部分绕 $\text{[math]}$ 旋转一周所形成的几何体的体积．

解答题普通

3. 如图，AB是圆柱 $\text{[math]}$ 的一条母线，BC过底而圆心O ， D是圆 $\text{[math]}$ 上一点．已知 $\text{[math]}$ ，

(1) 求该圆柱的表面积；

(2) 求 $\text{[math]}$ 的三边绕母线AB所在的直线旋转一周所围成的几何体的体积 $\text{[math]}$ ．

解答题普通