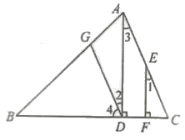
1.
已知  , 点
, 点  在
在  上, 点
上, 点  在
在  上, 点
上, 点  为射线
为射线  上一点.
上一点.

(1)
如图 1, 若  , 则
, 则  。
(2)
如图 2, 当点
。
(2)
如图 2, 当点  在线段
在线段  的延长线上时, 请写出
的延长线上时, 请写出  和
和  三者之间的数量关系, 并说明理由.
(3)
如图 3,
三者之间的数量关系, 并说明理由.
(3)
如图 3,  平分
平分  交
交  于点
于点  .
.
①若 平分
, 求
和
的数量关系;
②若 , 直接写出
的度数为 ▲
【考点】
角的运算;
平行线的判定与性质;
三角形的外角性质;
角平分线的概念;