1.
【问题提出】在旋转专题复习课中,王老师引导同学们积极探究以下问题:
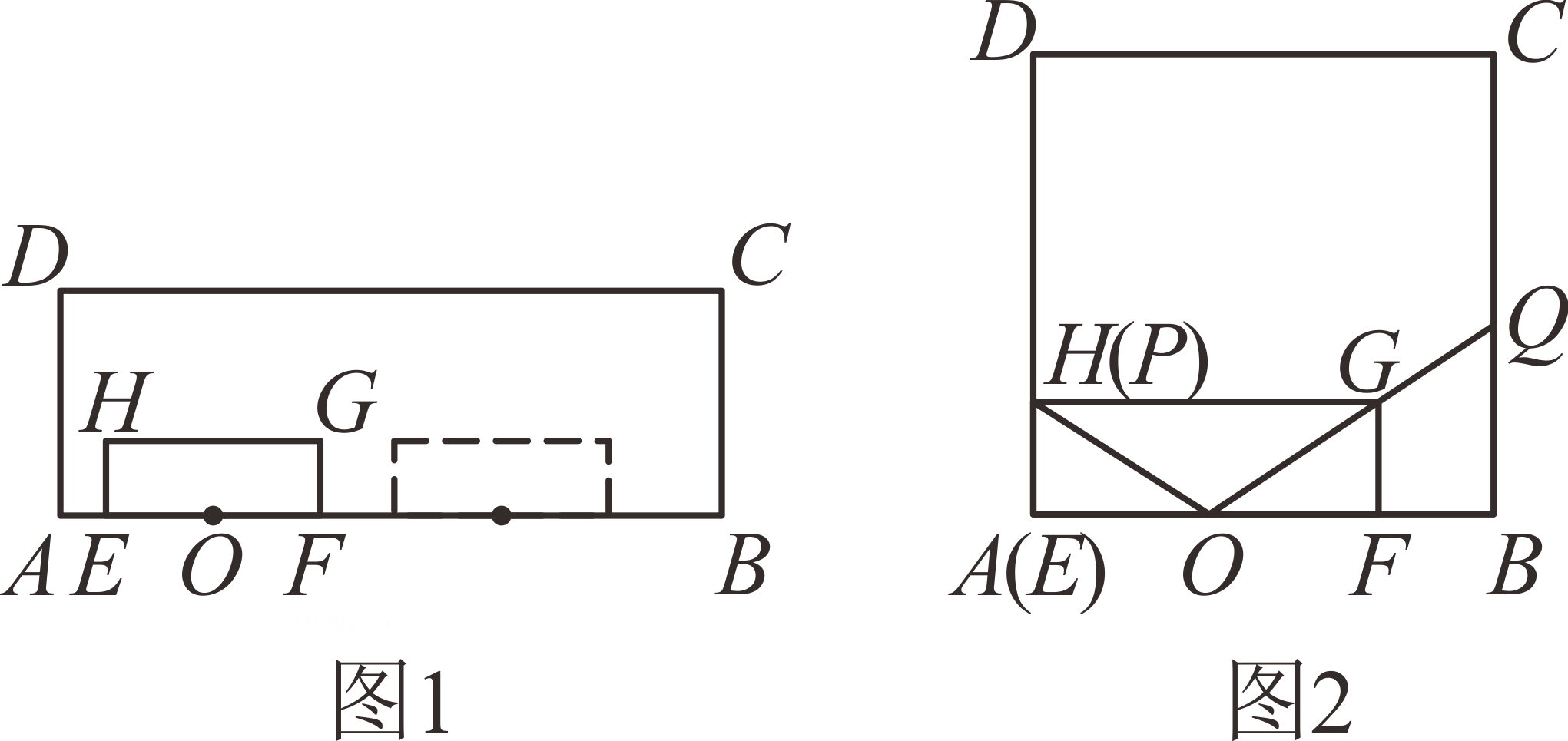
将一大一小两个等腰直角三角板如图1放置, , 点
在
内,连接BF并延长到点
, 使
BF,连接BD,CD,DE.探究线段DE与CD的关系.
【思路探究】
“勤学小组”的解题思路:将线段DE借助平行线进行平移,如图2,过点作BG平行DE交DF的延长线于点
, 这样可以将证明DE和CD的关系转化为BG和CD的关系:
“善思小组”的解题思路:结合为BE的中点构造三角形的中位线,如图3,过点
作BH平行DF交ED延长线于点
, 从而借助三角形中位线性质,将DE和CD的关系转化为DH和CD的关系.

(1)
请你写出线段DE与CD的关系并证明(写出一种方法即可);
(2)
【思维训练】
(3)
“【能力提升】
王老师为了进一步让学生体会平行线在图形证明中的作用,又出示了下列问题:
如图4,在中,
为AB上一点,将CD绕点
逆时针旋转
得到CE,连接BE,DE,O为DE中点,连接BO并延长交CD的延长线于点
, 若
, 探究OF,OB,BE之间的数量关系,并说明理由;
创新小组”的同学在【问题提出】的基础上对该问题又进一步拓展:连接CE,若F为平面内一点, , 其他条件不变,请直接写出AD的值.
【考点】
平移的性质;
相似三角形的判定与性质;
旋转的性质;
三角形的综合;
能力提升