如图，点C在以AB为直径的⊙O上，过点C作⊙O的切线l，过点A作AD⊥l，垂足为D，连接AC、BC．

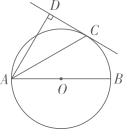
1. 如图，点C在以AB为直径的⊙O上，过点C作⊙O的切线l，过点A作AD⊥l，垂足为D，连接AC、BC．

(1) 求证：△ABC∽△ACD；

(2) 若AC＝5，CD＝4，求⊙O的半径．

【考点】

勾股定理; 切线的性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 如图，点B在以DE为直径的半圆上，A为圆心，连接AB ，设DC＝m ，且m＞n ．

(1) 请用m ， n表示Rt△ABC的三条边长．

(2) 若m ， n均为不超过20的正整数，且使Rt△ABC的三条边长都是整数，n的值．

解答题普通

2. 如图，锐角三角形ABC内接于圆O，过圆心O且垂直于半径OA的直线分别交AB、AC于点E、F. 设圆O在B、C两点处的切线交于点P.

证明：直线AP平分线段EF.

解答题困难

3. 如图，Rt△ABC中，∠C=90°，BC=3，点O在AB上，OB=2，以OB为半径的⊙O与AC相切于点D，交BC于点E，求弦BE的长．

解答题普通