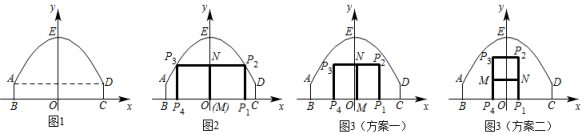
1.
【提出问题】
小星学习二次函数后,查阅资料发现其中一个抛物线形门洞,门洞内的地面宽度为两侧距地面
高处各有一盏灯.两灯间的水平距离为
, 未发现水泥门洞高度.他想知道这个门洞内部顶端离地面的距离为多少米.
【分析问题】
数形结合思想是解决问题的重要思想.小星想到建立适当的平面直角坐标系.通过数据求出二次函数的表达式.利用表达式可以求得这个门洞内部顶端离地面的距离为多少米.
【解决问题】

(1)
小星根据二次函数图象的性质建立了如图所示的平面直角坐标系.
(2)
小星学习小组的小红发现,如果她家遥控飞机模型(如图)能飞过此门洞是非常有趣的一件事,飞机的机翼长(是指左右两侧翼尖之间的总长度)为 , 为保障飞行安全.飞机水平飞行时高度必须控制在多少米以下?
(3)
为了造型更加美观,小星决定改造一下门洞,重新设计抛物线,其表达式为
, 为保障飞行安全.飞机水平飞行时高度必须控制在多少米以下?
(3)
为了造型更加美观,小星决定改造一下门洞,重新设计抛物线,其表达式为
 当
当 时,函数y的值总大于等于9.求b的取值范围.
时,函数y的值总大于等于9.求b的取值范围.
①求出抛物线的函数表达式;
②这个门洞内部顶端离地面的距离为多少米?
【考点】
待定系数法求二次函数解析式;
二次函数的实际应用-拱桥问题;
能力提升
真题演练