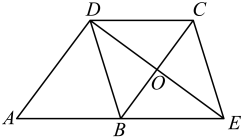
1.
如图, 现有一张矩形纸片  , 点
, 点  分别在矩形的边
分别在矩形的边  上. 将矩形纸片沿直线
上. 将矩形纸片沿直线  折叠, 使点
折叠, 使点  落在矩形的边
落在矩形的边  上, 记为点
上, 记为点  , 点
, 点  落在点
落在点  处,连结
处,连结  , 交
, 交  于点
于点  , 连结
, 连结  .
.

(1)
求证: 四边形  是菱形.
(2)
当点
是菱形.
(2)
当点  重合时, 求
重合时, 求  的长.
(3)
求
的长.
(3)
求  面积的取值范围.
面积的取值范围.
【考点】
等腰三角形的判定;
勾股定理;
菱形的判定与性质;
矩形的性质;
矩形翻折模型;