矩形ABCD中，点E、F分别在边CD、AB上，且DE=BF，∠ECA=∠FCA．

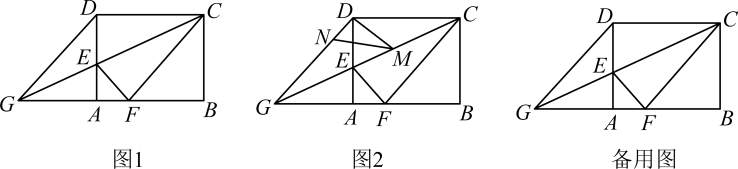
1. 矩形ABCD中，点E、F分别在边CD、AB上，且DE=BF，∠ECA=∠FCA．

(1) 求证：四边形AFCE是菱形；

(2) 若AB=8，BC=4，求菱形AFCE的面积．

【考点】

勾股定理; 菱形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， DE平分∠BDC交BC于点O，交AB的延长线于点E，连接CE．

(1) 求证：四边形BECD是菱形；

(2) 如果 $\text{[math]}$ ， $\text{[math]}$ ，求四边形BECD的面积．

综合题普通

2. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ 为 $\text{[math]}$ 边上的中线，过C点作 $\text{[math]}$ ，连接 $\text{[math]}$ ，且 $\text{[math]}$ ．

(1) 求证：四边形 $\text{[math]}$ 为菱形

(2) 若 $\text{[math]}$ ， $\text{[math]}$ ，求四边形 $\text{[math]}$ 的面积

综合题普通

3. 若一个四边形有一组邻边相等，且这组邻边夹角所对的对角线平分一个内角，则称这样的四边形为“近似菱形”，例如：如图1，在四边形ABCD中， $\text{[math]}$ ， BD平分 $\text{[math]}$ ，则四边形ABCD是近似菱形．

(1) 请在图2中作出一个以BD为对角线的“近似菱形”ABCD ，顶点A、顶点C要在网格格点上．

(2) 如图3，在四边形ABCD中， $\text{[math]}$ ，求证：四边形ABCD是“近似菱形”．

(3) 在（2）的条件下，若 $\text{[math]}$ ，求AB的长．

综合题困难