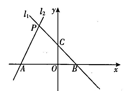
如图，直线与直线l2：y=kx+b交于点M（m ， 12），与y轴交于点P ，直线l2经过点（－6，0），且与y轴交于点Q ，直线y=a分别交y轴、直线l1、l2于A ， B ， C三点．

1. 如图，直线 $\text{[math]}$ 与直线l₂：y=kx+b交于点M（m ， 12），与y轴交于点P ，直线l₂经过点（－6，0），且与y轴交于点Q ，直线y=a分别交y轴、直线l₁、l₂于A ， B ， C三点．

(1) 求m的值及直线l₂的函数表达式；

(2) 当点A在线段PQ上（不与点P ， Q重合）时，若AB=2BC ，求a的值；

(3) 设点D（5，6）关于直线y=a的对称点为K ，若点K在直线l₁ ，直线l₂与x轴所围成的三角形内部（包括边界），求a的取值范围．

【考点】

待定系数法求一次函数解析式; 两一次函数图象相交或平行问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

1. 如图，在平面直角坐标系xOy中，过点 $\text{[math]}$ $\text{[math]}$ 的直线 $\text{[math]}$ 与直线 $\text{[math]}$ 相交于点 $\text{[math]}$ .

(1) 求直线 $\text{[math]}$ 的表达式；

(2) 过动点 $\text{[math]}$ 且垂直于 $\text{[math]}$ 轴的直线与 $\text{[math]}$ 的交点分别为C，D，当点 $\text{[math]}$ 位于点 $\text{[math]}$ 上方时，写出 $\text{[math]}$ 的取值范围.

解答题普通

2. 如图，已知过点B（1，0）的直线l₁与直线l₂：y=2x+4相交于点P（-1，a）.求：

(1) 直线l₂的函数表达式.

(2) 四边形PAOC的面积.

解答题普通

3. 在平面直角坐标系 $\text{[math]}$ 中，直线 $\text{[math]}$ ： $\text{[math]}$ 过 $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ ： $\text{[math]}$ ．

(1) 求直线 $\text{[math]}$ 的表达式；

(2) 过动点 $\text{[math]}$ 且垂直于 $\text{[math]}$ 轴的直线与 $\text{[math]}$ ， $\text{[math]}$ 的交点分别是 $\text{[math]}$ ， $\text{[math]}$ 当 $\text{[math]}$ 时，点 $\text{[math]}$ 位于点 $\text{[math]}$ 右方，直接写出 $\text{[math]}$ 的取值范围．

解答题普通