1.

(1)
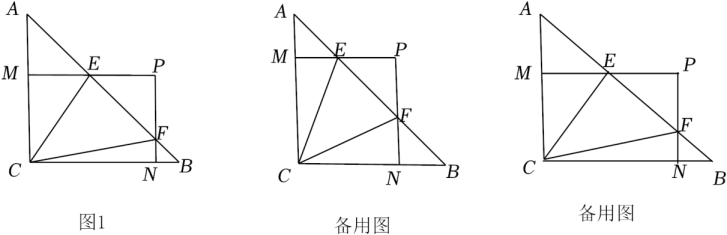
问题背景:小刚遇到一个这样问题:如图1,两条相等的线段 ,
,  交于点
交于点 ,
,  , 连接
, 连接 , 求证:
, 求证: . 通过尝试他发现通过平移可以解决这个问题
(2)
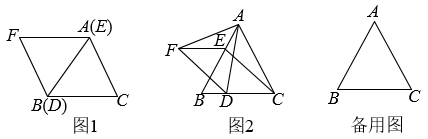
类比运用:如图2,
. 通过尝试他发现通过平移可以解决这个问题
(2)
类比运用:如图2, 与
与 相交于点
相交于点 ,
,  ,
,  ,
,  ,
,  ,
,  , 求线段
, 求线段 的长;
(3)
联系拓展:如图3,
的长;
(3)
联系拓展:如图3, 的三条中线分别为
的三条中线分别为 . 若
. 若 的面积为8,则以
的面积为8,则以 的长度为三边长的三角形的面积等于(请直接写出答案).
的长度为三边长的三角形的面积等于(请直接写出答案).
证明:过点作
且使
, 连接
,
∴四边形为平行四边形,则
,
∵ ,
∴ ,
又∵ ,
∴为等边三角形,
∴,
∴ , 即
.
请完成证明中的两个填空.并参考小刚同学思考的方法,解决下列问题:
【考点】
四边形的综合;
能力提升
真题演练