1.
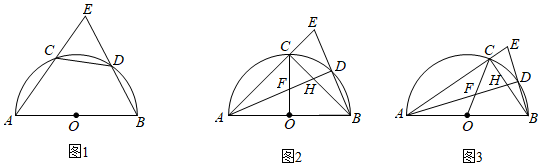
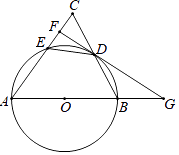
在 中,⊙O是
中,⊙O是 的外接圆,连结
的外接圆,连结 并延长,交
并延长,交 于点
于点 , 交⊙O于点
, 交⊙O于点 ,
,  . 连结
. 连结 ,
,  .
.

(1)
求证: .
(2)
求证:
.
(2)
求证: .
(3)
已知
.
(3)
已知 ,
,  , 是否能确定⊙O的大小?若能,请求出⊙O的直径;若不能,请说明理由.
, 是否能确定⊙O的大小?若能,请求出⊙O的直径;若不能,请说明理由.
【考点】
圆周角定理;
相似三角形的判定与性质;