如图，抛物线经过、两点，为抛物线上第一象限内的一个动点．

1. 如图，抛物线 $\text{[math]}$ 经过 $\text{[math]}$ 、 $\text{[math]}$ 两点， $\text{[math]}$ 为抛物线上第一象限内的一个动点．

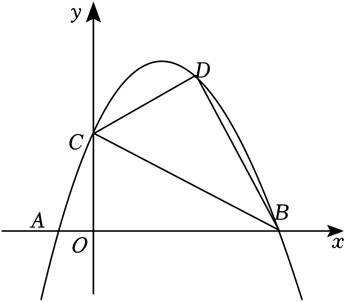
(1) 求抛物线所对应的函数表达式；

(2) 当 $\text{[math]}$ 的面积最大时，求点 $\text{[math]}$ 的坐标；

(3) 过点 $\text{[math]}$ 作 $\text{[math]}$ ，垂足为点 $\text{[math]}$ ，是否存在点 $\text{[math]}$ ，使 $\text{[math]}$ ，若存在，求点 $\text{[math]}$ 的横坐标；若不存在，请说明理由．

【考点】

二次函数的最值; 二次函数与一次函数的综合应用; 二次函数y=ax²+bx+c的图象; 二次函数y=ax²+bx+c的性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题困难

1. 已知：抛物线 $\text{[math]}$ ： $\text{[math]}$ .

(1) 若顶点坐标为 $\text{[math]}$ ，求b和c的值（用含a的代数式表示）；

(2) 当 $\text{[math]}$ 时，求函数 $\text{[math]}$ 的最大值；

(3) 若不论m为任何实数，直线 $\text{[math]}$ 与抛物线 $\text{[math]}$ 有且只有一个公共点，求a ， b ， c的值；此时，若 $\text{[math]}$ 时，抛物线的最小值为k ，求k的值.

综合题困难

2. 如图①，已知抛物线y₁＝x²+bx+c与x轴交于两点O（0，0）、A（2，0），将抛物线y₁向右平移两个单位长度，得到抛物线y₂ ．点P是抛物线y₁在第四象限内一点，连接PA并延长，交抛物线y₂于点Q ．

(1) 求抛物线y₂的表达式；

(2) 设点P的横坐标为x_P ，点Q的横坐标为x_Q ，求x_Q﹣x_P的值；

(3) 如图②，若抛物线y₃＝x²﹣8x+t与抛物线y₁＝x²+bx+c交于点C ，过点C作直线MN ，分别交抛物线y₁和y₃于点M、N（M、N均不与点C重合），设点M的横坐标为m ，点N的横坐标为n ，试判断|m﹣n|是否为定值．若是，直接写出这个定值；若不是，请说明理由．

综合题困难

3. 在暑假课后延时服务进行时，某班“数学兴趣小组”对函数 $\text{[math]}$ 的图象和性质进行了探究，探究过程如下，请补充完整．

(1) 自变量 $\text{[math]}$ 的取值范围是全体实数， $\text{[math]}$ 与 $\text{[math]}$ 的几组对应值列表如下：

$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	…
$\text{[math]}$	…	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	$\text{[math]}$	…

其中， $\text{[math]}$ ．

(2) 根据表中数据，在如图所示的平面直角坐标系中描点，并画出了函数图象的一部分，请画出该函数图象的另一部分．

(3) 观察函数图象，写出两条函数的性质．

(4) 进一步探究函数图象发现：

①函数图象与 $\text{[math]}$ 轴有个交点，所以对应的方程 $\text{[math]}$ 有个实数根．

②方程 $\text{[math]}$ 有个实数根．

③关于x的方程 $\text{[math]}$ 有2个实数根时， $\text{[math]}$ 的取值范围是．

综合题困难