1.
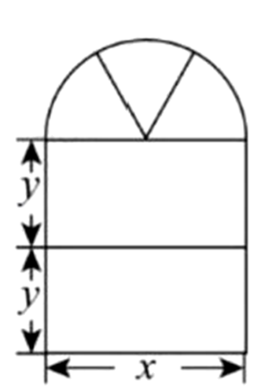
如图,一扇窗户,窗框为铝合金材料,上面是由三个大小相等的扇形组成 的半圆窗框构成,下面是由两个大小相等的长 , 宽
, 宽  的长方形窗框构成,窗户全部安装玻璃.(本题中
的长方形窗框构成,窗户全部安装玻璃.(本题中 取
取 , 长度单位为米)
, 长度单位为米)
铝合金(元/米) | 玻璃(元/平方米) | |
甲厂商 | 不超过 | |
乙厂商 |
|
(1)
一扇这样窗户 一 共需要铝合金多少米?(用含 的式子表示)
(2)
一扇这样窗户一共需要玻璃多少平方米?铝合金窗框宽度忽略不计(用含
的式子表示)
(2)
一扇这样窗户一共需要玻璃多少平方米?铝合金窗框宽度忽略不计(用含 的式子表示)
(3)
某公司需要购进
的式子表示)
(3)
某公司需要购进 扇这样的窗户,在同等质量的前提下,甲、乙两个厂商分别给出如表中报价,当
扇这样的窗户,在同等质量的前提下,甲、乙两个厂商分别给出如表中报价,当 时,该公司在哪家厂商购买窗户合算?
时,该公司在哪家厂商购买窗户合算?
【考点】
用代数式表示几何图形的数量关系;
能力提升


