1.
某校甲、乙两班参加植树活动．乙班先植树20棵，然后甲班才开始与乙班一起植树．设甲班植树的总量为
（棵），乙班植树的总量为
（棵），两班一起植树所用的时间（从甲班开始植树时计时）为x（时），
分别与x之间的部分函数图象如图所示．
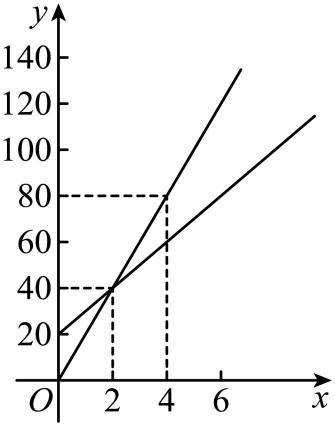
(1)
当
时，分别求与x之间的函数关系式．
(2)
如果甲、乙两班均保持前4个小时的工作效率，通过计算说明，当
时，甲、乙两班植树的总量之和能否超过180棵．
【考点】
待定系数法求一次函数解析式;
两一次函数图象相交或平行问题;
一次函数的实际应用;
能力提升
