1.
在Rt△ABC中,∠ABC=90°,AB=nBC , P为AB上的一点(不与端点重合),过点P作PM⊥AB交AG于点M , 得到△APM .

(1)
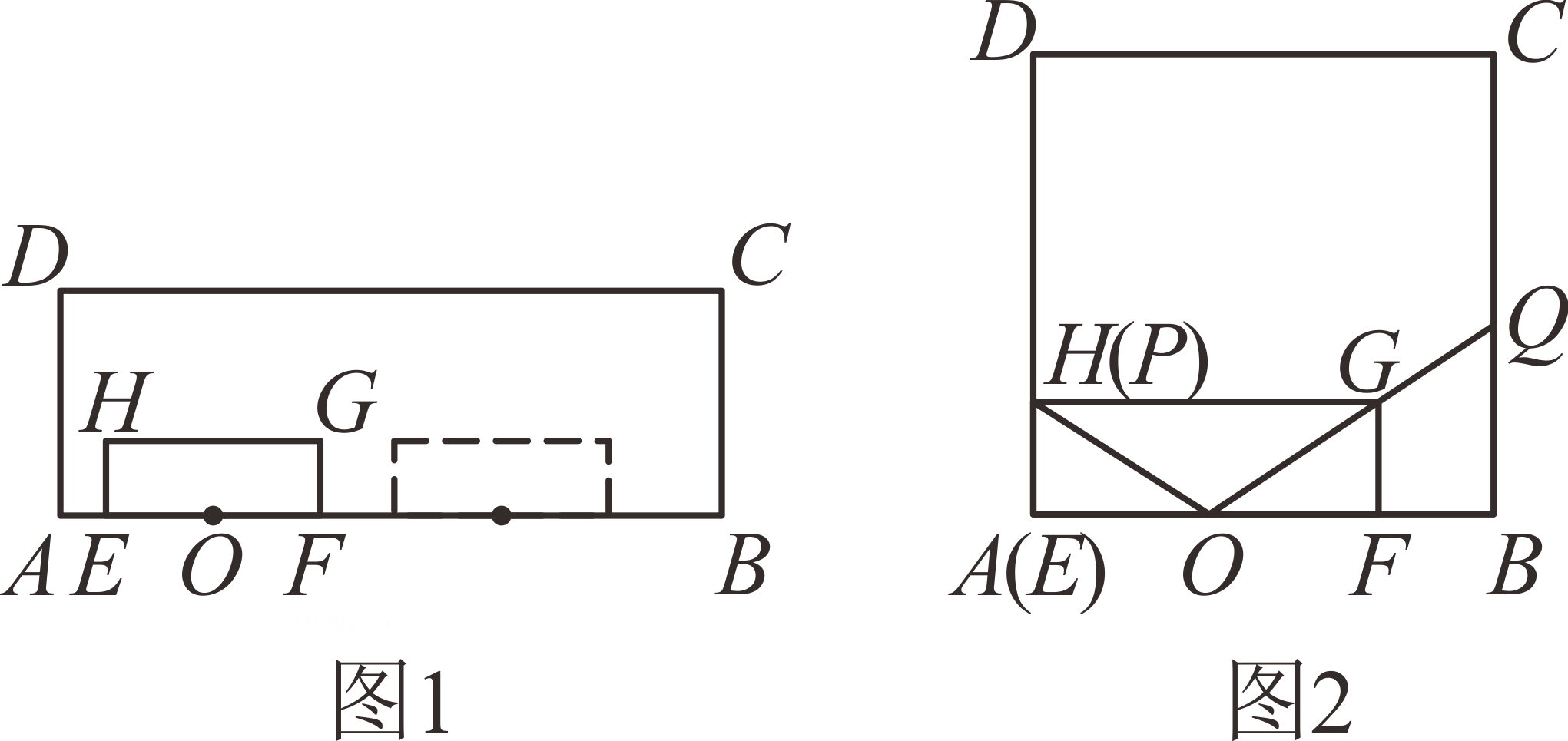
【问题发现】如图1,当n=1时,P为AB的中点时,CM与BP的数量关系为 ;
(2)
【类比探究】如图2,当n=2时,△APM绕点A顺时针旋转,连接CM , BP , 则在旋转过程中CM与BP之间的数量关系是否发生变化?请说明理由;
(3)
【拓展延伸】在(2)的条件下,已知AB=4,AP=2,当△APM绕点A顺时针旋转至B , P , M三点共线时,请直接写出线段BM的长.
【考点】
勾股定理;
相似三角形的判定与性质;
旋转的性质;
等腰直角三角形;
直角三角形的性质;
能力提升