【问题情境】如图，在△ABC中，∠ACB＝90°，AC＝kBC ， CD是AB边上的高，点E是DB上一点，连接CE ，过点A作AF⊥CE于F ，交CD于点G ．

1. 【问题情境】如图，在△ABC中，∠ACB＝90°，AC＝kBC ， CD是AB边上的高，点E是DB上一点，连接CE ，过点A作AF⊥CE于F ，交CD于点G ．

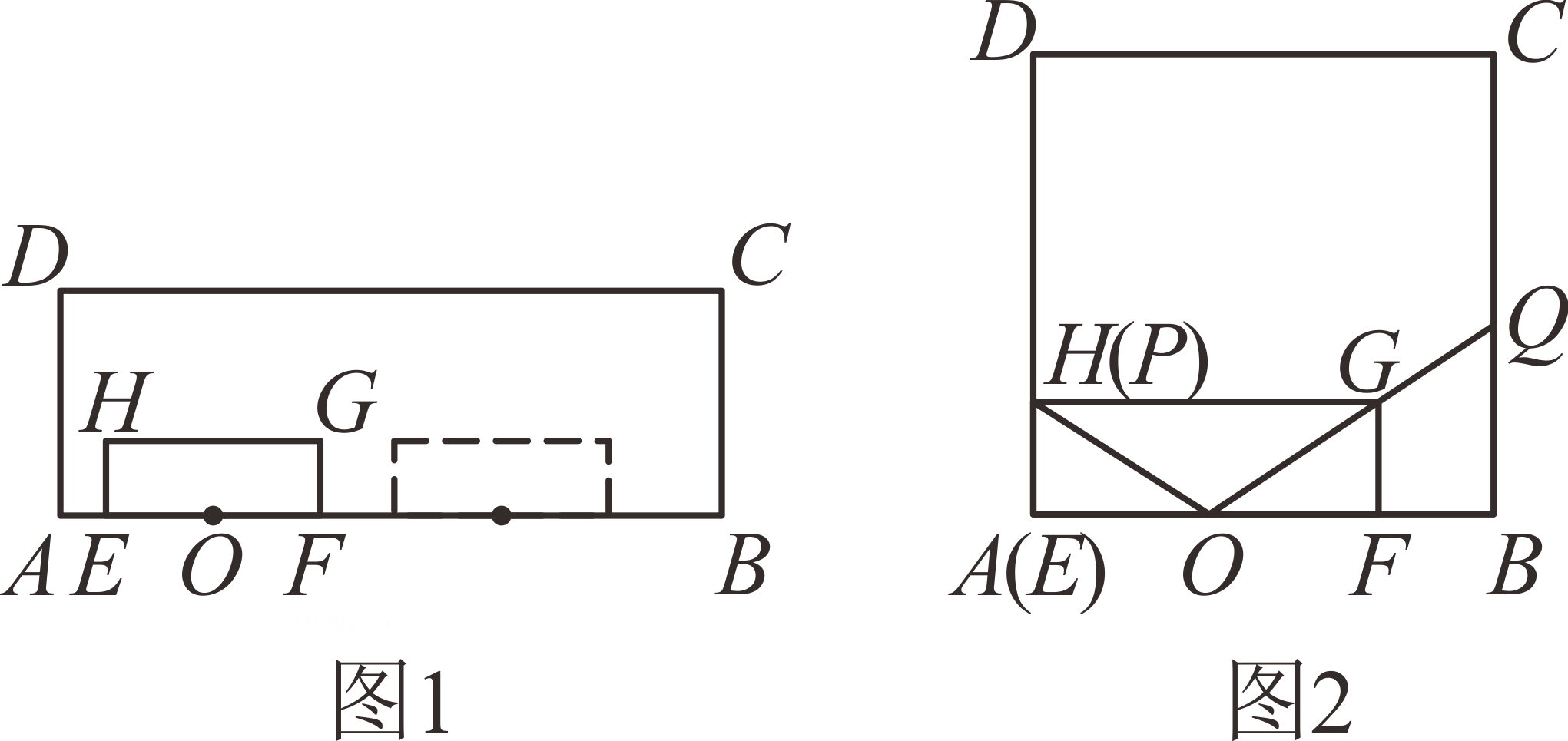
(1) 【特例证明】如图1，当k＝1时，求证：DG＝DE；

(2) 【类比探究】如图2，当 $\text{[math]}$ 时，（1）中的结论是否还成立？若成立，请写出证明过程，若不成立，请指出此时DG与DE的数量关系，并说明理由；

(3) 【拓展运用】如图3，连接DF ，若 $\text{[math]}$ ， AC＝AE ， DG＝3，求DF的长．

【考点】

直角三角形全等的判定-HL; 等腰三角形的性质; 相似三角形的判定与性质; 等腰直角三角形; 三角形全等的判定-ASA;

【答案】

您现在未登录，无法查看试题答案与解析。登录

实践探究题困难

1. 定义：如果四边形的一条对角线把该四边形分割成两个等腰三角形，且这条对角线是这两个等腰三角形的腰，那么我们称这个四边形为“双等腰四边形”。

(1) 如图①，在四边形ABCD中，∠BAD=∠BCD=90°，连结BD，E是BD的中点，连结AE，CE.

①试判断四边形ABCE是否为“双等腰四边形”，并说明理由.

②若∠AEC=90°，求∠ABC的度数.

(2) 如图②，E是矩形ABCD内一点，F是边CD上一点，四边形AEFD是“双等腰四边形”，且AD=DE.延长AE交BC于点G，连结FG.若AD=5， $\text{[math]}$ 求AB的长。

实践探究题困难

2. 如图1，小丽借助几何软件进行数学探究：第一步，画出矩形ABCD和矩形EFGH，点E，F在边AB上 $\text{[math]}$ ，且点C，D，G，H在直线AB的同侧；第二步，设置 $\text{[math]}$ ，矩形EFGH能在边AB上左右滑动；第三步，画出边EF的中点 $\text{[math]}$ ，射线OH与射线AD相交于点 $\text{[math]}$ （点 $\text{[math]}$ ， $\text{[math]}$ 不重合），射线OG与射线BC相交于点 $\text{[math]}$ （点Q，C不重合），观测DP，CQ的长度.

(1) 如图2，小丽取AB=4，EF=3，m=1，n=3，滑动矩形EFGH，当点E，A重合时，CQ=.

(2) 小丽滑动矩形EFGH，使得О恰为边AB的中点.她发现对于任意的m≠n，DP=CQ总成立.请说明理由.

(3) 经过数次操作，小丽猜想，设定m，n的某种数量关系后，滑动矩形EFGH，DP=CQ总成立.小丽的猜想是否正确？请说明理由.

实践探究题困难

(1) 问题背景：如图1，点E在BC上，AB⊥BC，AE⊥ED，DC⊥BC，求证： $\text{[math]}$ ＝ $\text{[math]}$ ．

(2) 尝试应用：如图2，在▱ABCD中，点F在DC边上，将△ADF沿AF折叠得到△AEF，且点E恰好为BC边的中点，求 $\text{[math]}$ 的值．

(3) 拓展创新：如图3，在菱形ABCD中，点E，F分别在BC，DC边上，∠AFE＝∠D，AE⊥FE，FC＝2．EC＝6．请直接写出cos∠AFE的值．

实践探究题困难