1.
如图,抛物线 经过点
经过点 和
和 .
.

(1)
求抛物线的函数表达式和对称轴.
(2)
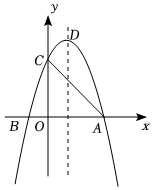
抛物线交 轴于点
轴于点 , 点
, 点 在线段OA上,过点
在线段OA上,过点 作
作 轴的平行线交抛物线于B,C两点(点B在点
轴的平行线交抛物线于B,C两点(点B在点 的左侧).若AP
的左侧).若AP , 求
, 求 的值.
的值.
【考点】
待定系数法求二次函数解析式;
二次函数图象上点的坐标特征;