1.
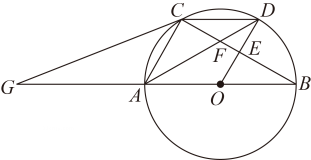
如图,AB是 的直径,弦
的直径,弦 于点E,G是
于点E,G是 上任意一点,连接AD,GD,AG.
上任意一点,连接AD,GD,AG.

(1)
找出图中和∠ADC相等的角,并给出证明;
(2)
已知BE=2,AE=8,求CD的长.
【考点】
勾股定理;
垂径定理;