1.
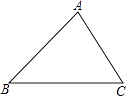
如图,在等边三角形ABC中,点 在直线BC上,连结AD,作
在直线BC上,连结AD,作 , 直线DN交射线AB于点
, 直线DN交射线AB于点 , 过点
, 过点 作
作 , 交直线DN于点
, 交直线DN于点 .
.

(1)
如图①,当点 在线段BC上,
在线段BC上, 为锐角时,求证:
为锐角时,求证:
 . (提示:过点
. (提示:过点 作
作 交射线AB于点
交射线AB于点 )
(2)
如图②,当点
)
(2)
如图②,当点 在线段BC的延长线上,
在线段BC的延长线上, 为锐角时,如图③,当点
为锐角时,如图③,当点 在线段CB的延长线上,
在线段CB的延长线上, 为钝角时,请分别写出线段CF,BE,CD之间的关系,不需要证明.
为钝角时,请分别写出线段CF,BE,CD之间的关系,不需要证明.
【考点】
平行线的性质;
等边三角形的性质;
平行四边形的判定与性质;