1.
将一副直角三角尺按如图1摆放在直线 上(直角三角尺
上(直角三角尺 和直角三角尺
和直角三角尺 ,
,  ,
,  ,
,  ,
,  , 保持三角尺
, 保持三角尺 不动,将三角尺
不动,将三角尺 绕点
绕点 顺时针方向转动.当
顺时针方向转动.当 转动至射线
转动至射线 上时,三角板
上时,三角板 停止转动.
停止转动.
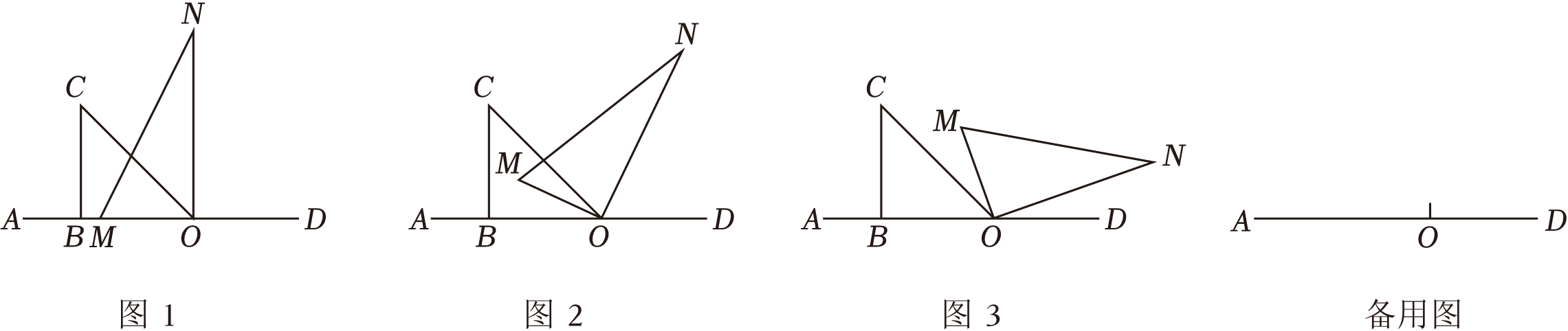
(1)
如图2,当 平分
平分 时,
时, 度.
(2)
三角尺
度.
(2)
三角尺 转动到如图3的位置,使得
转动到如图3的位置,使得 、
、 同时在直线
同时在直线 的右侧,猜想
的右侧,猜想 与
与 有怎样的数量关系?并说明理由.
(3)
在三角尺
有怎样的数量关系?并说明理由.
(3)
在三角尺 转动的过程中,是否存在
转动的过程中,是否存在 , 若存在,求出
, 若存在,求出 的度数,若不存在,请说明理由.
的度数,若不存在,请说明理由.
【考点】
角的运算;
余角、补角及其性质;
旋转的性质;
角平分线的概念;