1.
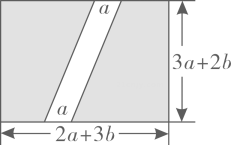
甲、乙两个长方形，其边长如图所示（
），其面积分别为
， 
．
(1)
用含m的代数式表示：
，
；（结果化为最简形式）
(2)
用“＜”、“＞”或“=”填空：；
(3)
若一个正方形的周长等于甲、乙两个长方形的周长之和，设该正方形的面积为
， 试探究：与
的差是否为定值？若为定值，请求出该值；如果不是，请说明理由．
【考点】
多项式乘多项式;
整式的混合运算;
