1.
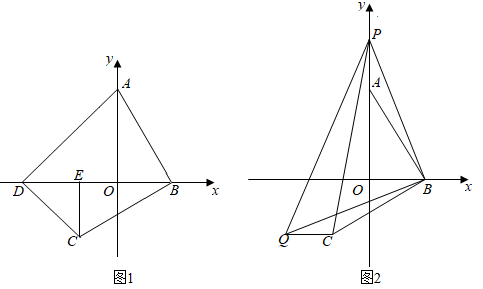
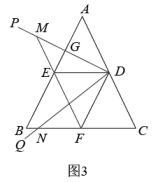
如图,在 中,
中, 于
于 于
于 相交于点O , 且
相交于点O , 且 .
.

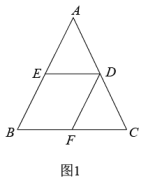
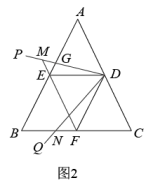
(备用图1) (备用图2)
(1)
求 °.
(2)
试说明:
°.
(2)
试说明: ;
(3)
点F是直线
;
(3)
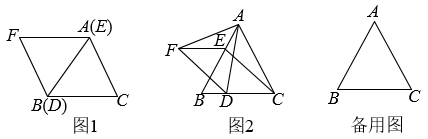
点F是直线 上的一点且
上的一点且 , 动点P从点O出发,沿线段
, 动点P从点O出发,沿线段 以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线
以每秒1个单位长度的速度向终点A运动,动点Q从点B出发沿射线 以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,问是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在,请在备用图中画出大致示意图,并求出符合条件的t值;若不存在,请说明理由.
以每秒4个单位长度的速度运动,P、Q两点同时出发,当点P到达A点时,P、Q两点同时停止运动.设点P的运动时间为t秒,问是否存在t值,使以点B、O、P为顶点的三角形与以点F、C、Q为顶点的三角形全等?若存在,请在备用图中画出大致示意图,并求出符合条件的t值;若不存在,请说明理由.
【考点】
三角形的综合;
能力提升
真题演练