1.
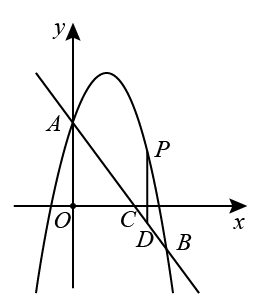
如图,抛物线 经过
经过 、
、 两点,点
两点,点 在该抛物线上运动,设点
在该抛物线上运动,设点 的横坐标为
的横坐标为 .
.

(1)
求该抛物线的解析式.
(2)
当 时,过点
时,过点 作
作 轴,交直线
轴,交直线 于
于 点,求线段
点,求线段 的最大值.
(3)
当
的最大值.
(3)
当 时,若抛物线在点
时,若抛物线在点 , 点
, 点 之间部分(包括点
之间部分(包括点 , 点
, 点 两个端点)的最高点和最低点的纵坐标的差为
两个端点)的最高点和最低点的纵坐标的差为 时,求
时,求 的值.
(4)
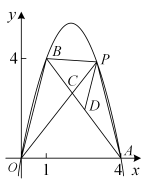
设抛物线
的值.
(4)
设抛物线 与线段
与线段 围成的封闭图形记作图形
围成的封闭图形记作图形 , 点
, 点 为直线
为直线 上的一个动点(点
上的一个动点(点 不与点
不与点 重合),设点
重合),设点 的横坐标为
的横坐标为 , 以
, 以 为边向下作正方形
为边向下作正方形 , 当
, 当 、
、 两点中只有一个点在图形
两点中只有一个点在图形 的内部时(不包括边界),直按写出
的内部时(不包括边界),直按写出 的取值范围.
的取值范围.
【考点】
二次函数的最值;
待定系数法求二次函数解析式;
二次函数与一次函数的综合应用;